Preslikavanje ravni pri kojem se svaka tačka A te ravni preslikava u tačku A’, simetričnu sa A u odnosu na pravu s te ravni, naziva se osnom simetrijom u odnosu na pravu (osu) s. Osna simetrija se još naziva i osna refleksija (ili samo refleksija). Najčešća oznaka za osnu simetriju je Is.
Za dve figure F i F’ neke ravni kaže se da su simetrične u odnosu na pravu s te ravni ako svakoj tački P figure F odgovara tačka P’ figure F’, tako da je Is (P) = P’. Naravno, važi i obrnuto, svakoj tački Q’ figure F’ odgovara tačka Q figure F, tako da je Is (Q’) = Q.
Primeri osnosimetričnih figura
Na slici ispod prikazane su figure sa jednom osom simetrije i sa više osa simetrije.
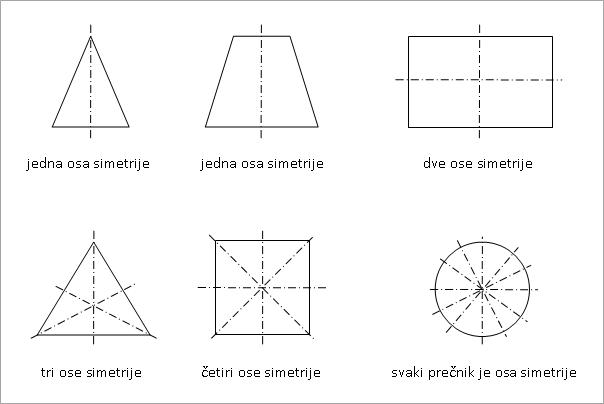
Kao što se vidi na slikama, jednakokraki trapez i jednakokraki trougao imaju po jednu osu simetrije, pravougaonik ima dve, jednakostranični trougao tri, a kvadrat četiri ose simetrije. Kod kruga je svaki prečnik osa simetrije.
Konstruisanje normale
Potrebno je iz date tačke A konstruisati normalu na datu pravu p (slika 1).
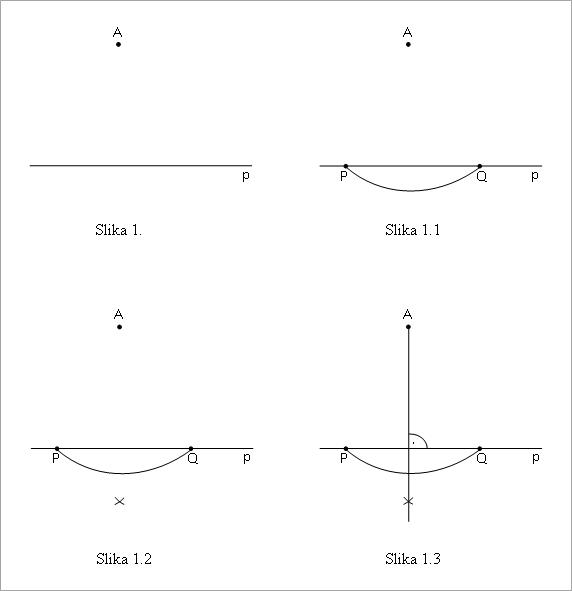
Prvo se iz tačke A šestarom opiše kružni luk na pravoj p, čime se dobijaju tačke P i Q (slika 1.1). Zatim se šestar postavi u tačku P, uzme otvor malo veći od polovine rastojanja PQ i opiše mali kružni luk; sa istim otvorom šestara opiše se mali kružni luk i iz tačke Q (slika 1.2). Kada se presek tih lukova spoji sa tačkom A, dobija se normala na pravu p (slika 1.3).
Primeri zadataka
1. Datoj duži AB konstruisati duž A’B’ simetričnu u odnosu na pravu s, koja ne seče datu duž (slika 2).
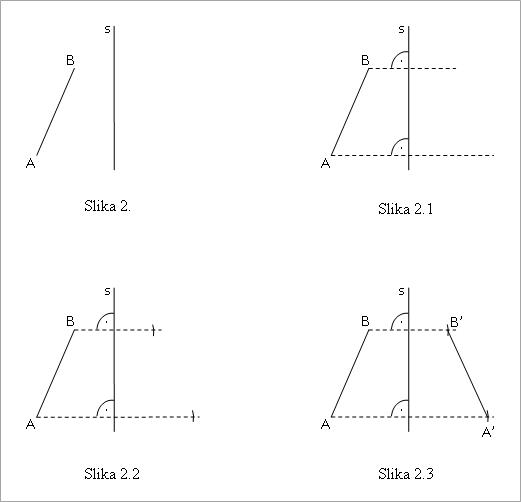
Prvo se iz tačaka A i B konstruišu normale na pravu s, koja predstavlja osu simetrije (slika 2.1). Zatim se šestar postavi u tačke u kojima normale seku pravu s i prebaci rastojanje do A, odnosno B, na drugu stranu (slika 2.2). Tako se dobijaju tačke A’ i B’, čijim spajanjem se dobija simetrična duž A’B’ (slika 2.3).
2. Dat je trougao ABC. Konstruisati njemu sličan trougao u odnosu na pravu s, koja sadrži teme B tog trougla i ne seče stranicu AC (slika 3).
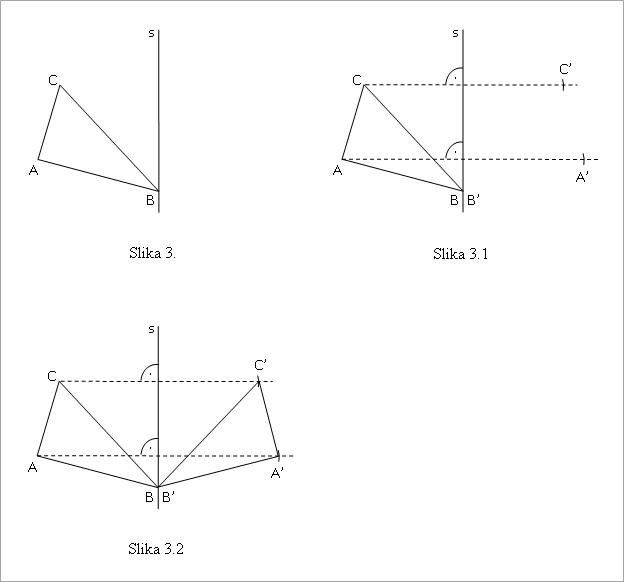
Ovde treba napomenuti: ako je tačka na osi simetrije, ona se ne preslikava, jer je njena osnosimetrična tačka ona sama (u ovom slučaju, B = B’).
Postupak je isti kao i u prethodnom primeru. Iz temena A i C konstruišu se normale na pravu s, a zatim se prebace rastojanja na njenu drugu stranu, čime se dobijaju tačke A’ i C’ (slika 3.1). Spajanjem konstruisanih tačaka dobija se trougao A’B’C’ (slika 3.2).