Trougao je figura u ravni ograničena sa tri strane. Zbir unutrašnjih uglova je 180°, a spoljašnjih 360°. Trouglovi se prema uglovima dele na oštrougle, pravougle i tupougle, a prema stranicama na raznostranične, jednakostranične i jednakokrake.
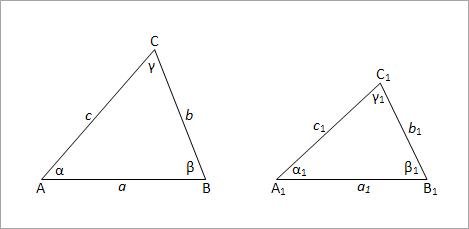
Dva trougla su podudarna (potpuno jednaka po obliku i veličini) ako imaju jednake odgovarajuće elemente – stranice i uglove. Ako su stranice jednog trougla a1, b1, c1 i uglovi α1, β1, γ1, a stranice drugog trougla a2, b2, c2 i uglovi α2, β2, γ2, oni će biti podudarni ako važi sledeće:
• a1 = a2, b1 = b2, c1 = c2 (jednake odgovarajuće stranice)
• α1 = α2, β1 = β2, γ1 = γ2 (jednaki odgovarajući uglovi)
Za dokazivanje podudarnosti dva trougla nije potrebno dokazati podudarnost svih stranica i svih uglova tih trouglova, već je dovoljno dokazati samo tri jednakosti. Za to se koriste četiri osnovna stava o podudarnosti trouglova. Ti stavovi su ravnopravni, a koji od njih će biti upotrebljen zavisi samo od podataka datih u zadatku.
1. Prvi stav o podudarnosti trouglova (SSS)
Dva trougla su podudarna ako i samo ako su stranice jednog trougla jednake odgovarajućim stranicama drugog trougla. Taj stav se kraće naziva SSS (stranica–stranica–stranica).
2. Drugi stav o podudarnosti trouglova (SUS)
Dva trougla su podudarna ako i samo ako su dve stranice jednog trougla i ugao zahvaćen njima jednaki odgovarajućim stranicama i uglu drugog trougla. Taj stav se kraće naziva SUS (stranica–ugao–stranica).
3. Treći stav o podudarnosti trouglova (USU)
Dva trougla su podudarna ako i samo ako imaju jednaku po jednu stranicu i oba odgovarajuća ugla nalegla na tu stranicu. Taj stav se kraće naziva USU (ugao–stranica–ugao).
4. Četvrti stav o podudarnosti trouglova (SSU)
Dva trougla su podudarna ako i samo ako su dve stranice jednog trougla i ugao naspram duže od njih jednaki odgovarajućim stranicama i uglu drugog trougla. Taj stav se kraće naziva SSU (stranica–stranica–ugao).