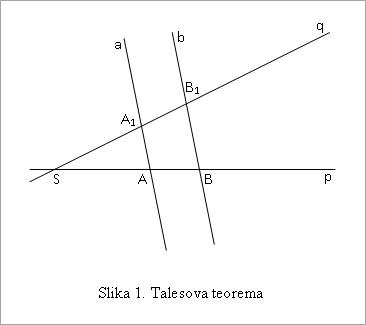
Ako paralelne prave a i b presecaju pravu p u tačkama A i B, a pravu q u tačkama A1 i B1, i ako je S zajednička tačka pravih p i q (slika 1), tada važi:
![]()
Na osnovu Talesove teoreme može se izvući sledeći zaključak: ako dve proizvoljne prave p i q preseca niz paralelnih pravih tako da su odsečci na jednoj pravoj međusobno jednaki, onda su i odsečci na drugoj pravoj međusobno jednaki.
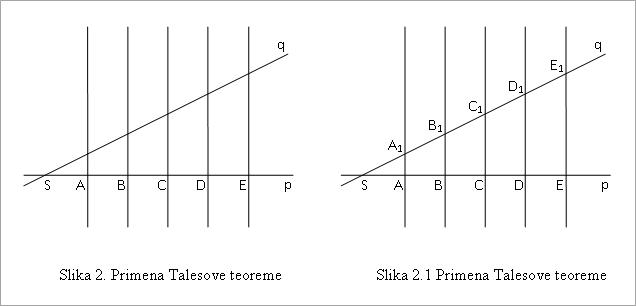
Na slici 2. se vidi niz paralelnih pravih koje prave jednake odsečke na polupravoj Sp, to jest AB = BC = CD = DE. Onda su i odsečci na polupravoj Sq (slika 2.1), po Talesovoj teoremi, takođe jednaki, to jest A1B1 = B1C1 = C1D1 = D1E1.