Dve jednačine sa dve nepoznate kod kojih su rešenja tih nepoznatih ista čine sistem jednačina. Pod sistemom od dve linearne jednačine sa dve nepoznate, x i y, podrazumeva se:
a1 · x + b1 · y = c1
a2 · x + b2 · y = c2
To je takozvani prost sistem, gde su a1, b1, c1, a2, b2, c2 dati realni brojevi (ponekad i parametri). Rešenje sistema je uređeni par brojeva (x0, y0), za koji važi da je:
a1 · x0 + b1 · y0 = c1
a2 · x0 + b2 · y0 = c2
Ako u zadatku nije dat sistem u opštem obliku, potrebno ga je ekvivalentnim transformacijama svesti na taj oblik. U tom smislu, treba obratiti pažnju da se iste nepoznate uvek pišu jedne ispod drugih radi preglednosti i lakšeg snalaženja u sistemu. Tipovi ekvivalentnih transformacija za jednakost A = B jesu:
1. A + c = B + c
2. A − c = B − c
3. A · c = B · c
4. A : c = B : c, c ≠ 0
Sistemi jednačina mogu se rešiti pomoću više metoda: zamena, suprotni koeficijenti, grafički, determinante itd. Svi metodi dovode do istog rešenja, a koji će se od njih koristiti zavisi od postavke zadatka (treba izabrati onaj metod koji se u datom zadatku učini najpogodnijim za rešavanje).
Sistemi jednačina kod kojih postoji samo jedno rešenje (tj. jedan uređeni par rešenja) nazivaju se određeni sistemi. Osim njih postoje i neodređeni sistemi (sistemi koji imaju beskonačno mnogo rešenja) i kontradiktorni (nemogući) sistemi (sistemi koji nemaju nijedno rešenje).
Metod zamene
Postupak: izabrati jednu od dve date jednačine i iz nje izraziti jednu od nepoznatih preko druge nepoznate, a zatim tu nepoznatu u drugoj jednačini zameniti dobijenim izrazom. Na taj način dobija se jedna jednačina sa jednom nepoznatom.
Savet: prilikom odabira nepoznate treba izabrati onu koja ispred sebe ima koeficijent (broj) koji olakšava račun.
Primeri zadataka
1. Rešiti sistem jednačina:
x + 3y = 25
2x − 5y = −27
U jednoj od jednačina treba izraziti jednu nepoznatu preko svega ostalog. Druga jednačina se samo prepiše. U ovom slučaju, najlakše je izraziti x iz prve jednačine.
x = 25 − 3y
2x − 5y
Sada se prva jednačina prepisuje, a u drugoj umesto nepoznate x stavlja ono što je jednako x, a to je u ovom slučaju 25 − 3y. Na taj način druga jednačina postaje jednačina sa jednom nepoznatom, pa je lako izračunati tu nepoznatu.
x = 25 − 3y
2 · (25 − 3y) − 5y = −27
Izraz koji menja x je stavljen u zagradu jer se čitav taj izraz množi brojem 2, koji stoji uz x. Ostatak zadatka je običan račun.
x = 25 − 3y
50 − 6y − 5y = −27
x = 25 − 3y
50 − 11y = −27
x = 25 − 3y
−11y = −27 − 50
x = 25 − 3y
−11y = −77
x = 25 − 3y
y = −77/(−11)
x = 25 − 3y
y = 7
Sada treba u prvoj jednačini umesto y napisati dobijeni broj i izračunati drugu nepoznatu, tj. x.
x = 25 − 3 · 7
y = 7
x = 25 − 21
y = 7
x = 4
y = 7
Rešenje sistema jednačina je uređeni par brojeva: (x, y) = (4, 7).
Provera: zamenom ta dva rešenja u obe jednačine sistema dobijaju se dobre jednakosti.
4 + 3 · 7 = 25
2 · 4 − 5 · 7 = −27
4 + 21 = 25
8 − 35 = −27
25 = 25
−27 = −27
2. Rešiti sistem jednačina:
2x + 4y = 8
5x + y = −7
U jednoj od jednačina treba izraziti jednu nepoznatu preko svega ostalog. Druga jednačina se samo prepiše. U ovom slučaju, najlakše je izraziti y iz druge jednačine.
2x + 4y = 8
y = −7 − 5x
Sada se druga jednačina prepisuje, a u prvoj umesto nepoznate y stavlja ono što je jednako y, a to je u ovom slučaju −7 − 5y. Na taj način prva jednačina postaje jednačina sa jednom nepoznatom, pa je lako izračunati tu nepoznatu.
2x + 4 · (−7 − 5x) = 8
y = −7 − 5x
Izraz koji menja y je stavljen u zagradu jer se čitav taj izraz množi brojem 4, koji stoji uz y. Ostatak zadatka je običan račun.
2x − 28 − 20x = 8
y = −7 − 5x
−18x −28 = 8
y = −7 − 5x
−18x = 8 + 28
y = −7 − 5x
−18x = 36
y = −7 − 5x
x = 36/(−18)
y = −7 − 5x
x = −2
y = −7 − 5x
Sada treba u drugoj jednačini umesto x napisati dobijeni broj i izračunati drugu nepoznatu, tj. y.
x = −2
y = −7 − 5 · (−2)
x = −2
y = −7 + 10
x = −2
y = 3
Rešenje sistema jednačina je uređeni par brojeva: (x, y) = (−2, 3).
Provera: zamenom ta dva rešenja u obe jednačine sistema dobijaju se dobre jednakosti.
2 · (−2) + 4 · 3 = 8
5 · (−2) + 3 = −7
−4 + 12 = 8
−10 + 3 = −7
8 = 8
−7 = −7
Metod suprotnih koeficijenata
Postupak: pomnožiti jednačine odgovarajućim brojem kako bi koeficijenti ispred jedne od nepoznatih u obe jednačine bili isti brojevi, ali sa suprotnim znacima. Zatim sabrati date jednačine.
Savet: izabrati nepoznatu ispred koje su koeficijenti (brojevi) „laki” za račun.
Primeri zadataka
1. Rešiti sistem jednačina:
2x + 3y = 34
8x − 6y = −8
Potrebno je da ispred jedne nepoznate budu isti brojevi, ali sa suprotnim znacima. U ovom slučaju, najbolje je prvu jednačinu pomnožiti sa 2 (tako se uz y dobija 6 i −6).
2x + 3y = 34 /·2
8x − 6y = −8
4x + 6y = 68
8x − 6y = −8
Sada treba sabrati te dve jednačine i izračunati nepoznatu x.
12x + 0y = 60
12x = 60
x = 60/12
x = 5
Kada se nađe jedno rešenje, treba se vratiti u jednu jednačinu (bilo koju) da bi se našlo drugo rešenje.
2x + 3y = 34
2 · 5 + 3y = 34
3y = 34 − 10
3y = 24
y = 24/3
y = 8
Rešenje sistema jednačina je uređeni par brojeva: (x, y) = (5, 8).
Provera: zamenom ta dva rešenja u obe jednačine sistema dobijaju se dobre jednakosti.
2 · 5 + 3 · 8 = 34
8 · 5 − 6 · 8 = −8
10 + 24 = 34
40 − 48 = −8
34 = 34
−8 = −8
2. Rešiti sistem jednačina:
5x − y = 1
10x − 2y = 2
Prva jednačina množi se sa −2.
5x − y = 1 /·(−2)
10x − 2y = 2
−10x + 2y = −2
10x − 2y = 2
Sada se jednačine sabiraju.
0x + 0y = 0
0 = 0
To znači da je sistem jednačina neodređen, odnosno da ima beskonačno mnogo rešenja. Da bi se ta rešenja opisala, iz jedne od jednačina treba izraziti x ili y, zavisno od toga šta je lakše.
5x − y = 1
y = 5x − 1
Sada su rešenja: (x, y) = (x, 5x − 1); x ∈ R.
3. Rešiti sistem jednačina:
9x + 15y = 6
−9x − 15y = 12
Jednačine se odmah sabiraju.
0x + 0y = 18
0 = 18
To znači da je sistem jednačina nemoguć, odnosno da nema rešenja.
4. Rešiti sistem jednačina:
ax − 10y = 15a
2ax + 5y = 5a
U ovom zadatku postoji parametar a. Postupak je isti.
ax − 10y = 15a
2ax + 5y = 5a /·(−2)
ax − 10y = 15a
4ax + 10y = 10a
Sada se jednačine sabiraju i izračunava nepoznata x.
5ax + 0y = 25a
5ax = 25a
x = 25a/5a
x = 5
Napomena: a se može skratiti samo ako je a ≠ 0 (to je uslov).
Sada se x zameni u jednoj od jednačina (bilo kojoj) da bi se našlo y.
ax − 10y = 15a
5a − 10y = 15a
−10y = 15a − 5a
−10y = 10a
y = 10a/(−10)
y = −a
Rešenja su: (x, y) = (5, −a), uz uslov a ≠ 0.
Šta se dešava ako je a = 0?
Kada se ta vrednost zameni u početni sistem jednačina, dobija se:
ax − 10y = 15a
2ax + 5y = 5a
0x − 10y = 15 · 0
0x + 5y = 5 · 0
−10y = 0
5y = 0
Ovde se vidi da je y = 0, a x može biti bilo koji broj. To znači da je sistem neodređen, odnosno da ima beskonačno mnogo rešenja (y = 0, x ∈ R).
Grafički metod
Postupak: nepoznate u svakoj od jednačina sistema su linearno zavisne, pa se svaka od njih može predstaviti grafički. To znači da je potrebno konstruisati grafike (prave) za svaku od datih jednačina.
Savet: radi jednostavnijeg konstruisanja grafika, nepoznatu y treba izraziti iz datih jednačina.
Primeri zadataka
1. Rešiti sistem jednačina:
2x + 3y = 5
3x + y = −3
Prvo se iz prve jednačine izrazi y.
2x + 3y = 5
3y = −2x + 5
y = −2x/3 + 5/3
Sada se za najmanje dve vrednosti x izračuna vrednost y, što se, najčešće, daje u vidu tabele. Potom se nacrta grafik za prvu jednačinu.
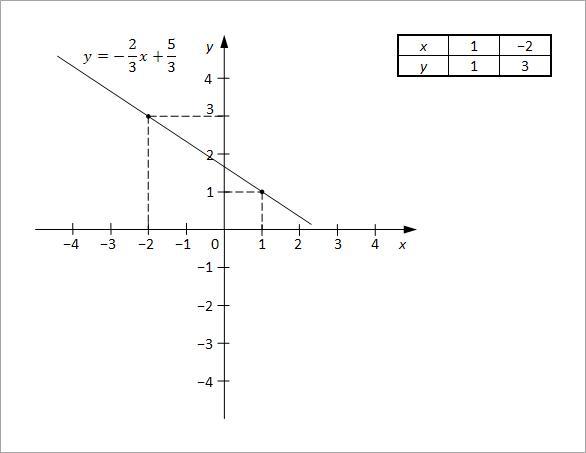
Sada se iz druge jednačine izrazi y.
3x + y = −3
y = −3x − 3
Sada se za najmanje dve vrednosti x izračuna vrednost y. Potom se nacrta grafik za drugu jednačinu.
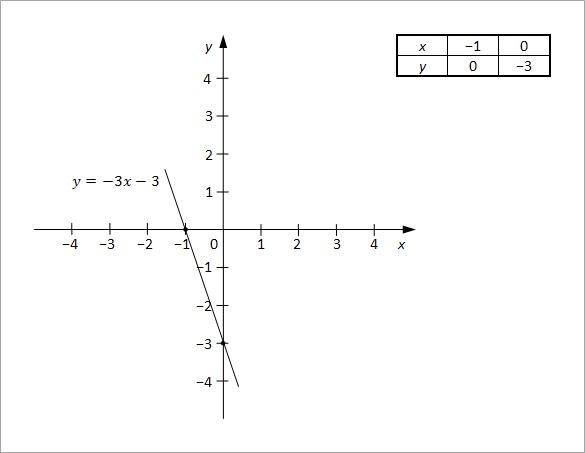
Rešenje sistema jednačina je tačka nastala u preseku pravih.
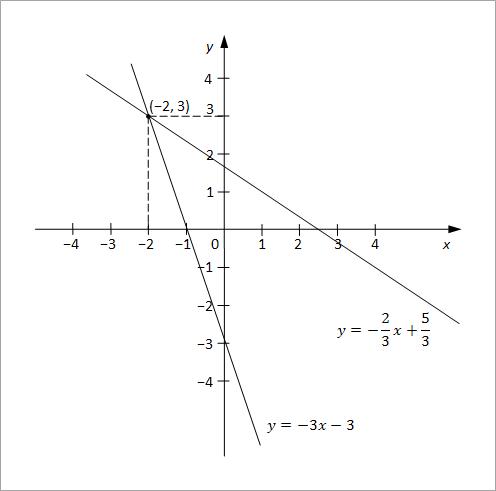
Rešenje sistema jednačina je uređeni par brojeva: (x, y) = (−2, 3).
2. Rešiti sistem jednačina:
2x − y = 3
−2x + y = 6
Prvo se iz prve jednačine izrazi y.
2x − y = 3
y = 2x − 3
Sada se za najmanje dve vrednosti x izračuna vrednost y, što se, najčešće, daje u vidu tabele. Potom se nacrta grafik za prvu jednačinu.
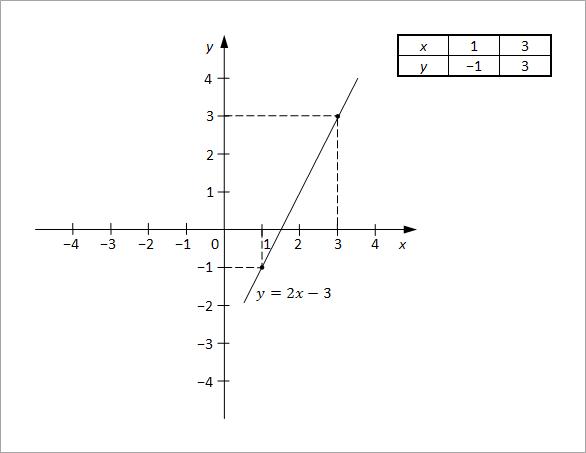
Sada se iz druge jednačine izrazi y.
−2x + y = 6
y = 2x + 6
Sada se za najmanje dve vrednosti x izračuna vrednost y. Potom se nacrta grafik za drugu jednačinu.
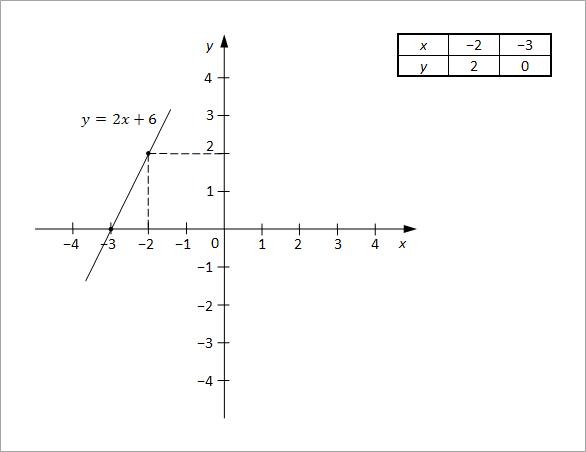
Rešenje sistema jednačina je tačka nastala u preseku pravih.
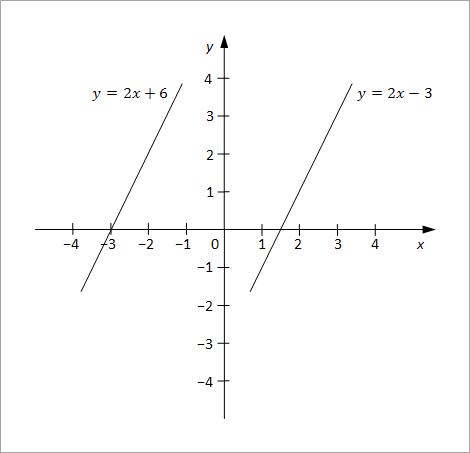
Prave su paralelne, tako da ne postoji presečna tačka. To znači da je sistem jednačina nemoguć, odnosno da nema rešenja.