Pomoću velikog večitog kalendara može se utvrditi dan u nedelji za svaki poznati datum u periodu od 1. do 2399. godine, bez obzira na to da li je u pitanju gregorijanski ili julijanski kalendar. Primena gregorijanskog kalendara u Španiji, Portugaliji i Papskoj državi u Italiji počela je 5. oktobra 1582. godine, tako što je eliminisano deset dana, a 5. oktobar postao je 15. oktobar.
Svaka godina deljiva sa 4 je prestupna, osim godina koje su deljive sa 100, ali sa izuzetkom onih koje su deljive sa 400. To znači da godine 1700, 1800, 1900, 2100, 2200. i 2300. nisu prestupne (jer su deljive sa 100, ali ne i sa 400), dok godine 1600, 2000. i 2400. jesu prestupne (jer su deljive sa 400).
Da bi se pronašao traženi dan, treba poći od slova u tabeli 1, u kojoj su označeni vekovi i godine. Dva slova u koloni označavaju prestupnu godinu; prvo slovo upotrebljava se za januar i februar, a drugo za ostale mesece. Dalji postupak se sastoji u tome da se u tabeli 2 pronalazi kolona u kojoj stoji slovo označene godine. To slovo je u istom redu sa mesecom za koji se upotrebljava kalendar. Ta kolona označava i dane u nedelji, koji se upotrebljavaju zajedno sa mesecom.
Tabela 1
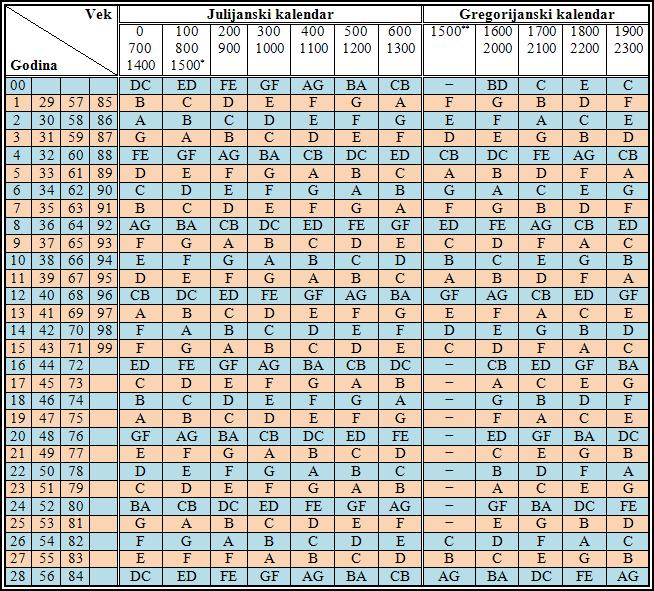
Napomena: Za XVI vek, za datume pre 5. oktobra 1582. koristi se julijanski kalendar (1500*), dok se za datume posle 15. oktobra 1582. koristi gregorijanski kalendar (1500**).
Tabela 2
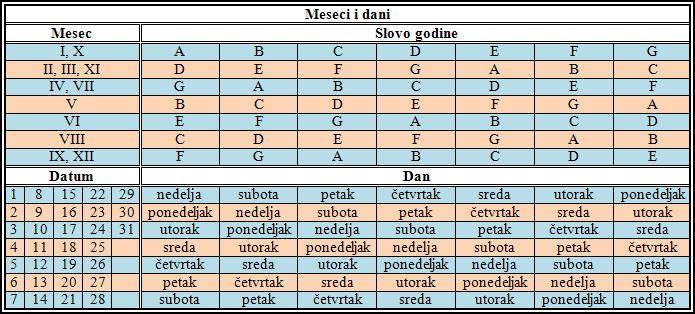
Primeri
• 5. decembar 1981. godine
Prvo se u tabeli 1 pronalazi slovo koje označava 1981. godinu – slovo D. Zatim se u tabeli 2 u redu u kojem se nalazi dvanaesti mesec u godini pronalazi kolona u kojoj stoji slovo D. Ta kolona označava i dan u nedelji koji se traži, a koji se nalazi u redu u kojem je peti dan u mesecu. Tako ispada da je 5. decembra 1981. bila subota.
• 16. oktobar 2003. godine
Prvo se u tabeli 1 pronalazi slovo koje označava 2003. godinu – slovo E. Zatim se u tabeli 2 u redu u kojem se nalazi deseti mesec u godini pronalazi kolona u kojoj stoji slovo E. Ta kolona označava i dan u nedelji koji se traži, a koji se nalazi u redu u kojem je šesnaesti dan u mesecu. Tako ispada da je 16. oktobra 2003. bio četvrtak.
• 19. februar 2120. godine
Prvo se u tabeli 1 pronalazi slovo koje označava 2120. godinu – slovo G. Zatim se u tabeli 2 u redu u kojem se nalazi drugi mesec u godini pronalazi kolona u kojoj stoji slovo G. Ta kolona označava i dan u nedelji koji se traži, a koji se nalazi u redu u kojem je devetnaesti dan u mesecu. Tako ispada da će 19. februara 2120. biti ponedeljak.